UCM-History
Authors: Marijn Hafkamp (AMU), Anaëlle Cheillan (UL), Prof. Raoul Bongers (UMCG)
The following REPAIRS toolbox is available under the CC-BY licence (Creative- Commons: https://creativecommons.org/). This implies that others are free to share and adapt our works under the condition that appropriate credit to the original contribution (provide the name of the REPAIRS consortium and the name the authors of the toolbox when available, and a link to the original material) is given and indicate if changes were made to the original work.
A Historical Overview of the Origin and Applications of the Uncontrolled Manifold Analysis in Human Movement Behaviour
Background information document to the UCM Toolbox
The uncontrolled manifold analysis (UCM) is an analysis technique to determine whether the elements of a movement system stabilize a chosen performance variable in a discrete or rhythmic motor task (Scholz & Schöner 1999). In this contribution we provide background information about the origin and the applications of the UCM analysis over the years. The overview is presented in two chapters. In the first chapter, we describe the scientific context within which the UCM was introduced to the field of human movement science. Moving from the observations of Bernstein to the rise of Dynamical Systems Approach and beyond, this text explains why the UCM was introduced and its contribution to the field of motor control. In the second chapter, we explain how the uncontrolled manifold analysis matured to a well-established analysis of human movement variability. In the 20 years after its introduction, the uncontrolled manifold analysis has been exploited and further developed by various labs all over the world. By giving an overview of the different tasks, populations and contexts to which the UCM has been applied, we aim to demonstrate the potential of this analysis to understand the control of human movement.
The origin of the uncontrolled manifold analysis in the study of human movement
The uncontrolled manifold hypothesis (UCM) was introduced to the field of movement science in 1995 by Gregor Schöner, who transformed this hypothesis into an analysis technique in 1999, together with John Scholz (Scholz & Schöner, 1999). Even though the theoretical concept of a solution manifold was already known in the field of robotics – under the name of ‘self-motion’ (e.g. Burdick et al. 1989, Murray et al. 1994) – the idea to use an uncontrolled manifold to analyze human movement was new. Rapidly after its introduction, the UCM gained attraction and different research labs began to use the method. In short, the objective of a UCM analysis is to calculate whether the elements of a movement system stabilize a self-chosen performance variable in the execution of a discrete or rhythmic motor task. For example, a UCM analysis informs about the extent to which the joints of the arm and shoulder compensate for each other to stabilize the tip of your finger in a pointing task (e.g. Valk et al. 2019). This is done by partitioning the trial-to-trial variability of the systems’ elements (i.e. the joints) into variance that does and variance that does not affect the state of the performance variable (i.e., the tip of the index finger). More technically the variance is partitioned into variance orthogonal and parallel to a task-specific manifold in a state space that is spanned by the elements of the movement system relevant for the task. The method filled a gap in the methodological toolbox of movement scientists and therefore it added to conceptual developments in thinking about the control of human movement (e.g., Latash et al. 2007, Riley et al. 2011).
The goal of the first part of this background document is to clarify why the concept of an uncontrolled manifold was introduced to the study of human movement. In order to reach this goal, we take a few steps back and present this clarification in the context of a short historical overview of the field of motor control. To this end we answer the question, which observations or theoretical steps have led to the postulation of the UCM hypothesis? On our journey through the field’s history, we will see the rise of Dynamical Systems Theory in movement science (DST, e.g., Haken et al. 1985, Saltzman & Kelso 1987, Turvey 1990). This perspective on human movement was pioneered by studies on rhythmic action, emphasizing the importance of understanding stability in movements and developing tools to assess properties of stability. It was in this context that the concept of an uncontrolled manifold provided the tools to make crucial steps from rhythmic to discrete movements in assessing stability and its counterpart, the underlying variance of the constituting system elements. In the years after its introduction, the UCM proved its value by being applied to a variety of different tasks, populations and contexts (see chapter 2). However, all of this started with an observation of the Soviet scientist Nikolai Bernstein.
Almost 100 years ago, Bernstein (re-published 1967) observed that hammering movements never exactly repeat themself, although the hammer consistently lands on approximately the same point. Bernstein noticed that even the most skilled laborers display much more variability in their joint angle configurations than in the landing of the end-point of the hammer, suggesting that the variability in the joint angles does not form a substantial problem in the control of the hammer throws. This finding was regarded to be remarkable, since the general assumption at the time was that highly skilled agents display repeatable, robot-like motor performances. In the decades after this observation, studies have shown similar behavioral patterns in pointing and grasping tasks. The end-effector, often being the finger or a hand, shows a trajectory with typical characteristic and accurately lands on the target even though joint angle configurations are highly variable during the movement. Hands move in approximately straight lines during unperturbed reaching, and the velocity profiles are always nearly bell-shaped (Morasso 1981), regardless of the various (starting) configurations of the arm. These observations suggest that our neuromotor system puts higher controldemandson the end-effector trajectory than on the other elements that constitute the movement system, such as the joint angles. We appear to control the end-effector of our movement system in the action, while the elements generating the movement system are allowed to be more variable than the end-effector.
In line with this insight, in 1982, Kelso and colleagues published an observation that added to our thinking about the control of the elements in our movement system. In a study on speech behavior, Kelso et al. (1982) found that the elements of our speech system (i.e., the tongue, lips and jaws) immediately compensated for the perturbation of another element in a way that the function (i.e., the produced sound) was preserved. In other words, the elements demonstrated functional compensation, providing the speech system with an intrinsic stability against small perturbations. This finding suggested that the elements of a movement system might cooperate to resist small disturbances so that performance outcome is maintained –a function or a particular end-effector trajectory. This implies that individual elements of the movement system are not independent, but they covary in a compensatory way to stabilize the function, such as the end-effector trajectory in a reaching movement.
Partly inspired by theories of Bernstein (1967) and the perceptual psychologist Gibson (1979) and developments in the fields of physics, chemistry and mathematics, in the 1980s the field of human movement science saw the rise of a new theoretical perspective on the study of motor control and action-perception coupling: The Dynamic Systems Theory (DST, e.g., Turvey 1990, Beek et al. 1995). Driven by the theoretical concepts of Synergetics (Haken, 1977), such as order parameters, self-organization and circular causality, the Haken-Kelso-Bunz-model of rhythmic movements (Haken, Kelso & Bunz 1985) soon provided a paradigm to study movement behavior. In this upcoming perspective, Saltzman & Kelso (1987) proposed a Task Dynamic Approach: an innovative theoretical framework that formulated an explanation for (a) consistency of end-effector trajectories and (b) functional compensation of the underlying elements of a movement system. In the tradition of DST, self-organized action units formed the core of this approach: task-specific ‘devices’ are formed, in which several elements of the neuromotor system cooperate to perform a function. For example, a hammering device, to fulfill the task of hammering, can consist of all the joint angles in the trunk, arm and hand. Within the Task Dynamic Approach these action units emerge in the performance of a task, and they are specified in a low-dimensional state space (also: ‘action space’). Specification in a state space means that the end-effector trajectory of the action unit is represented by a dynamical topology in that space. In the example of the rhythmic hammering, the tip of the hammer can be represented by a limit cycle in a two-dimensional state space (position vs. velocity of the hammer).
This novel, abstract description of the movement behavior provides a global representation of the dynamics of the system as a whole. By using this approach, Saltzman & Kelso (1987) were able to contextualize and explain the consistency of the end-effector trajectory and the functional compensation of individual elements. To successfully complete a movement task such as hammering, the end-effector trajectory is by far the most relevant element to control. Hence, the control of the hammering movement is directed at stabilizing the trajectory of the tip of the hammer, keeping the trajectory in state space close to the limit cycle. In other words, the limit cycle in state space forms an attractor that attracts the action unit to a stable rhythm. Accuracy of the tip of the hammer is preserved by creating a hammering action unit in which the individual joints functionally compensate for each other to stabilize the hammer on its way.
The task-dynamical framework of Saltzman and Kelso (1987) had an original and novel perspective on the organization and control of our neuromotor system in that self-organizing task-specific action units were claimed to be at the core of motor coordination. This deviated from the at that time more conventional approaches in motor control relying on motor programs or neurophysiological explanations. However, in the late eighties the approach was still in its infancy, and it needed to be broadened to provide a more extensive explanation of movement behavior. The primary focus of this perspective had been on movements in the rhythmic domain, as exemplified by the paradigmatic HKB model (1985) for rhythmic finger coordination. Stability of rhythmic movements could be visualized by the amount of variability in state space: the trajectories in state space either remain close to a limit cycle (stable) or diverted from the limit cycle (unstable). Unfortunately, it was problematic to apply this technique to discrete movements, such as grasping or pointing, because these movements do not follow a limit cycle regime (but see Schöner, 1991 for an exception of modelling discrete movements using a limit cycle). Therefore, to analyze stability properties of discrete movements a different method had to be used. The challenge was to find a way to assess whether the elements of an action unit compensated for each other to stabilize an end-effector during movements such as discrete pointing, as argued from a Task Dynamics Perspective. A major issue to examine stability in a reaching movement is that variability at the level of the end-effector (i.e., the hammer) is measured in different units than variability in the body parts that bring about those movements, such as the joint angles of the arm and shoulder (Schöner, 1995).
Gregor Schöner recognized these problems (1995) and made the crucial steps that enabled to examine stability properties of discrete movements. The neuromotor system, so he argued, not only stabilizes the end-effector pattern during the execution of a rhythmic movement, but also during the performance of discrete movements. Moreover, during a movement, all configurations of the system that do not affect the stability of the end-effector pattern are ‘free to vary’. He took the example of a pointing movement, with the finger as end-effector, to explain this idea:
“(…) although the end-effector pattern is controlled, there are directions in which the limb configurations (the combinations of joint angles) are not controlled – namely those directions that leave the end-effectors invariant (or a subset of those).”
It was this step – the distinction of element configurations that stabilize (or: control) and those that do not stabilize the end-effector – that opened the route to connecting the variance of the system elements, to the variance of the end-effector. Together this allowed to assess stability properties of discrete movements. Following the concept of self-motion in robotics (e.g. Burdick et al. 1989, Murray et al. 1994), Schöner proposed that the set of limb configurations that leave the end-effector invariant are located on a manifold in a large state space made up by the task-relevant elements: the uncontrolled manifold. This state space could span all of the relevant elements of the movement system under analysis. For example, during a pointing movement the individual joints of the arm and shoulder could form the state space. Note here the difference with the notion of state space of Saltzman & Kelso (1987): instead of a state space spanned by the position and velocity of an end-effector, state space of the UCM is formed by the elements of the movement system. This state space links the task-relevant system elements to the end-effector. Exploiting the UCM idea of state space enables a movement scientist to divide trial-to-trial movement variance of system elements into components that are either parallel or orthogonal to the uncontrolled manifold. In other words, the variance of these elements either stabilizes or destabilizes the end-effector trajectory. Hence, with this method it was possible to analyze the stability of a discrete movement.
In 1999 Scholz and Schöner first applied the concept of an uncontrolled manifold by analyzing the movement variability in a discrete sit-to-stand task. They used the UCM analysis to investigate whether the joint angles of the body stabilized either the center of mass (CM), the head position or the hand position, throughout the sit-to-stand movement. To examine these different hypotheses, a state space was created, spanned by the different joint angles of the body. In this high-dimensional state space, for each individual performance variable (such as the CM) unique manifolds were calculated on which joint configurations would leave that performance variable unaffected: the uncontrolled manifolds. When the movement unfolds, this manifold continuously changes. The method allows to compute at each point in time of the movement the trial-to-trial variability of the joint angles, parted in variability orthogonal to the manifold and variability parallel to the manifold. The orthogonal variability of the joints – often labelled VORT – affects the performance, while the parallel variability – the VUCM – does not affect the performance variable. If the parallel component of variance is consistently larger than the orthogonal component, it is commonly agreed that the joint angles ‘stabilize’ the end-effector. The analyses of Scholz and Schöner (1999) demonstrated that the joint angles compensated for each other to stabilize the CM over time, rather than head or hand position, and a new movement analysis technique was presented to the field.
The goal of this first chapter was to clarify why the concept of an uncontrolled manifold was introduced to the study of human movement. We have described the context in which the UCM was introduced, that is, the rising of a dynamical systems approach to movement control and coordination. In a field where the large majority of the empirical and theoretical work was devoted to understanding stability of rhythmic movements, the UCM provided a technique to analyze stability (and hence control) of discrete movements. This uncontrolled manifold analysis enables us to understand why a hammer can land on the exact same spot with every repetition albeit the exact movements are not repeated. Even though the joint angles of the upper body have the freedom to vary, there are limits to this variation. As long as this variance is largely parallel to the uncontrolled manifold in state space with relation to the end-effector, the hammer will land on the same spot. In the second chapter of this contribution, we will provide an overview of the applications of the uncontrolled manifold hypothesis to the field of human movement science in the 20 years after its introduction, with the aim to show its potential value to understand motor control.
The applications of the uncontrolled manifold analysis to human movement
In the first part of this article, we explained how the uncontrolled manifold analysis can provide a deeper understanding of structure of variability in human movement. Using this method, variability in elements of a movement system that produce discrete movements, can be partitioned into variability that stabilizes and variability that destabilizes a specific performance variable. Note here that this performance variable, as well as the elements that are hypothesized to covary, are selected by the researcher. This allows testing for the hypothesized control of a set of different variables in the same analysis, as already demonstrated by Scholz & Schöner (1999) when introducing the UCM analysis. They did this by computing the ratio of VUCM and VORT for different performance variables during a sit-to-stand task, hypothesizing that the performance variable for which this ratio was the highest, can be regarded as the controlled variable. They showed that the joint angles of the body compensate for each other to stabilize – and hence control – the position of the center of mass in the sagittal plane, rather than the head or hand position in space. In the years following this seminal publication, the UCM approach has not only been applied to new tasks and contexts, but research groups have also utilized the analysis to investigate covariation of elements at other levels of a movement system than merely the joint angle level. For instance, Latash et al. (e.g. 2001, 2002) has used the analysis to investigate the covariation of force production tasks and Passos et al. (2018, 2019) have analyzed covariation in velocity vectors of players in team sports. The current chapter is aimed at providing a brief and broad overview of the different applications of the uncontrolled manifold analysis over the years. Moreover, we aim to give some insight into the different theoretical frameworks to interpret the results of a UCM analysis.
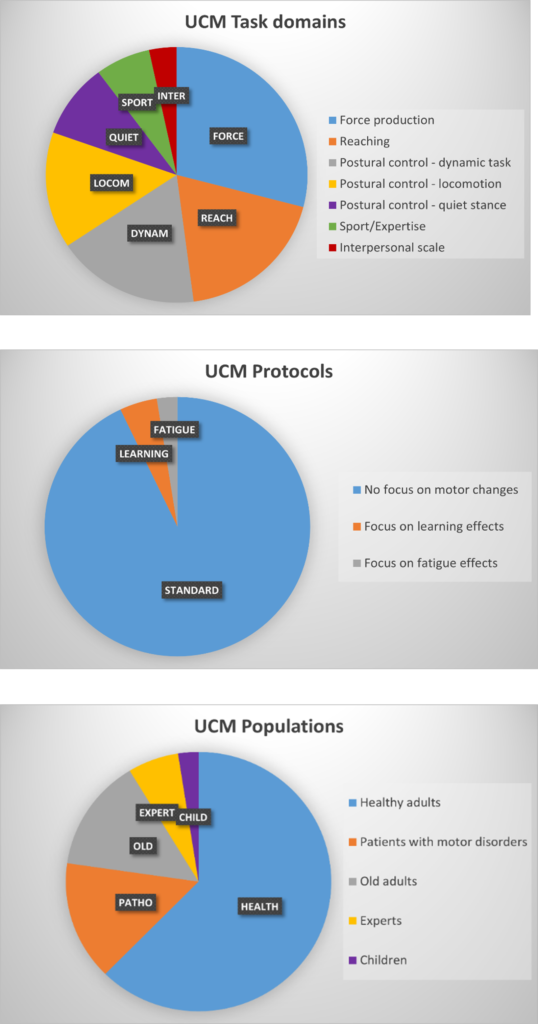
Soon after its introduction, the uncontrolled manifold analysis attracted the attention of human movement scientists that studied a large variety of motor tasks. The UCM was used to analyze movement variability in pointing and reaching tasks (e.g., Scholz et al., 2000; Domkin et al., 2002, 2005; Van der Steen et al. 2011; Wissing et al., 2020); force production tasks (e.g., Latash et al., 2001, 2002; Kang et al., 2004; Madarshahian et Latash, 2021); postural control during quiet stance (e.g., Krishnamoorthy et al., 2003, 2004, 2005; Reimann et Schöner, 2017); locomotion (e.g., Robert et al., 2009; Qu, 2012; Monaco et al., 2018) and other, more dynamic movement tasks (e.g., Scholz et al., 2001; Auyang et al., 2008; DiCesare et al., 2020). In all those studies, motor control was studied in terms of a performance variable that was to be stabilized by task-relevant system elements. To give some examples, joint angles were hypothesized to stabilize an end-effector position during pointing (such as Wissing et al. 2020), finger forces were expected to stabilize a total target force (e.g. Latash et al. 2001) and muscle modes were assumed to stabilize the center of pressure (Krishanamoorty et al., 2003).
The various examples mentioned above demonstrate the potential of the UCM to capture general mechanisms of motor control that apply to different tasks and contexts. It is important to mention, however, that the outcome measures of the UCM have been interpreted in different ways, depending on the theoretical framework of the research. One of the most common and influential interpretations of the UCM analysis that we like to spend a few words on, is related to the concept of ‘synergies’. Synergies have been defined differently over the years (for good overview see: Bruton & O’Dwyer, 2018 and Profeta & Turvey, 2017), but they are generally assumed to couple elements of a system so as to decrease the number of degrees of freedom. In other words, synergies make a redundant system controllable (Bernstein 1967). In this context, the concept of an uncontrolled manifold is interesting and sheds a different light on the control of these redundant degrees of freedom. The UCM enables to establish the extent to which elements vary to compensate each other with respect to a to-be-stabilized performance variable. This means that the analysis offers a tool to understand how elements are functionally coupled. For this reason, Latash et al. (2007) suggest UCM analysis as a tool that is very well suited to analyze whether elemental variables are coupled in synergies. In this definition, synergies do not only couple elements to facilitate control, but this coupling is functional and specifically aimed at stabilizing a variable emphasizing that the degrees of freedom are not redundant but abundant. Latash et al (2007) suggested that a stabilization of a performance variable, which is indicated by VUCM being larger than VORT, shows the presence of a synergy. Having said this, it is worth mentioning that many studies utilising the UCM refrain from mentioning the concept of a synergy, limiting their interpretation to ‘structure in movement variability’ (e.g., Hsu et al., 2007; Scholz et al., 2012; Park et al., 2016; Reimann et Schöner, 2016; Martin et al., 2019).
Other than applying the uncontrolled manifold analysis to investigate motor control in different tasks, the method has also been used to study movement variability in a variety of populations, such as children (e.g., reaching: Golenia et al., 2018; force production: Shaklai et al., 2017; postural control: Wu et al., 2009; Beerse et Wu, 2019); older adults (e.g., reaching: Krüger et al., 2013; Greve et al 2013, 2019; force production: Shinohara et al., 2004; postural control: Freitas et Duarte, 2012; Sit-to-stand: Greve et al 2017); and people with various pathologies and injuries, including Down’s syndrome (e.g., Scholz et al., 2003); Parkinson’s disease (e.g., Park et al., 2013, 2014); stroke (e.g., Reisman et Scholz, 2006); and knee osteoarthritis (e.g., Shafizadegan et al., 2022, 2022). In general, these studies found support for the idea that aging and injuries/pathologies can lead to altered couplings between the movement system’s elements, ultimately resulting in atypical or destabilized movement patterns. This illustrates that an UCM analysis can provide a good depiction of the body’s changing functionality, forming a potentially useful tool for the assessment of motor development, rehabilitation techniques or healthy ageing.
More recently, the UCM method has also been used in the context of sports and (motor) expertise. In contrast with the complex movement skills that are often required in such settings, the majority of the studies focused on simplified or basic motor tasks. For instance, expert surgeons’ skills have been assessed in a two-dimensional reaching task using two targets (Nisky et al., 2014) and parkour experts were asked to jump and land on a target landmark placed on the floor (Maldonaldo et al., 2018). Traditionally, to perform the UCM analysis certain constraints are added to ensure consistent joint configurations at the start and end positions of the task. These constraints enable the accurate computation of UCM variables and their comparison across trials. However, such constraints potentially modify the natural movement or require reduction of complex motor skills as performed by experts to a more simplistic version. A small number of studies have used the UCM analysis in more contextualized, realistic tasks, in which no experimental constraints were added. To give an example, the UCM has been applied in archery (Serrien et al., 2018) and basketball shooting (Hasanbarani et Latash, 2020; Nakano et al., 2022), where the goal of those sport activities can be phrased as ‘reaching a task-specific target with a task-specific object’. A flake in stone knapping (Rein et al., 2013) or a ball in tennis table forehand (Iino et al., 2017) can also be classified hitting task-specific targets. Some studies to sport specific movements have specifically focused on multi-joint coordination, such as the UCM analysis of a golf swing (Morrison et al., 2016). The authors demonstrated that the variability of the arm’s joint angles was functionally structured to minimize the variability of the end-effector trajectory, where the end-effector was – in this case – the clubhead. Moreover, the UCM has also been used to investigate postural control in an ecological context. In Montull and colleagues’ UCM-based study (2020), standing on a slackline was described as maintaining balance on a task-specific unstable surface. Lastly, the UCM has been adopted in more rhythmic sports behavior, such as human gait and expert running (Möhler and colleagues, 2019, 2020, 2021, 2022); swimming (Sanders et al., 2020) and dribbling (Robalo et al., 2021).
This overview of the tasks, populations and contexts that have been investigated using the uncontrolled manifold analysis, highlights the opportunities of employing this method to better understand human movement behavior. As demonstrated in this chapter, the UCM not only allows to investigate the stabilization of different performance variables in one task, but its general form also invites the user to apply the method to a variety of systems in which elements are hypothesized to covary with respect to a performance variable. Making use of this large conceptual freedom, some groups have also attempted to use the UCM analysis to investigate coordination on an interpersonal scale (e.g. Riley et al. 2011, Passos et al. 2018). Interpersonal coordination is a scientific topic well-documented in the literature, as it occurs in a wide range of contexts such as social events, animal colonies, teamwork, sport and other daily life situations. In the future this will be presented in a separate toolbox: “Interpersonal coordination and the UCM”. To end this overview of the UCM and its use, Appendix 1 presents three charts in which the different domains of focus of the UCM from the past 20 years is indicated.
Conclusion
The goal of this contribution was to provide background information about the uncontrolled manifold analysis to help students of movement sciences to understand the added value of this technique. In the first part, we explained how the UCM was initially introduced to analyse stability and variability in discrete motor tasks, filling the gap that was left by the common analysis techniques that were used by proponents of a dynamical systems approach to motor control. In the second part of this paper, we showed that the use of the UCM is by no means restricted to the analysis of joint angle variability in discrete movement tasks. In contrast, our overview demonstrates that the UCM can be used to analyse a large range of systems. In fact, the take home message of this contribution is that the UCM is in principle applicable to any system in which elements are assumed to covary in order to stabilize a variable. This message is illustrative in the recent explorative studies to interpersonal coordination, wherein different individuals are assumed to covary their actions to stabilize a performance variable together
References
Auyang, A. G., Yen, J. T., & Chang, Y.-H. (2009). Neuromechanical stabilization of leg length and orientation through interjoint compensation during human hopping. Experimental Brain Research, 192(2), 253‑264.
Beek, P.J., Peper, C.E., & Stegeman, D.F (1995). Dynamical models of movement coordination. Human Movemement Science. 14: 573-608.
Beerse, M., & Wu, J. (2019). Neuromechanical control of leg length and orientation in children and adults during single-leg hopping. Experimental Brain Research, 237(7), 1745‑1757.
Bernstein, N. A. (1967). The co-ordination and regulation of movements. New York, NY: Pergamon Press. 1-196.
Burdick, J.W. (1989). On the inverse kinematics of redundant manipulators: characterization of the self-motion manifolds. Advanced Robotics. 25-34.
DiCesare, C. A., Bonnette, S., Myer, G. D., & Kiefer, A. W. (2020). Differentiating Successful and Unsuccessful Single-Leg Drop Landing Performance Using Uncontrolled Manifold Analysis. Motor Control, 24(1), 75‑90.
Domkin, D., Laczko, J., Djupsjöbacka, M., Jaric, S., & Latash, M. L. (2005). Joint angle variability in 3D bimanual pointing : Uncontrolled manifold analysis. Experimental Brain Research, 163(1), 44‑57.
Domkin, D., Laczko, J., Jaric, S., Johansson, H., & Latash, M. L. (2002). Structure of joint variability in bimanual pointing tasks. Experimental Brain Research, 143(1), 11‑23.
Freitas, S. M. S. F., & Duarte, M. (2012). Joint coordination in young and older adults during quiet stance : Effect of visual feedback of the center of pressure. Gait & Posture, 35(1), 83‑87.
Gibson, J.J. (1979). The Ecological Approach to Visual Perception. Boston: Houghton Mifflin.
Golenia, L., Bongers, R. M., van Hoorn, J. F., Otten, E., Mouton, L. J., & Schoemaker, M. M. (2018). Variability in coordination patterns in children with developmental coordination disorder (DCD). Human Movement Science, 60, 202‑213.
Golenia, L., Schoemaker, M. M., Otten, E., Mouton, L. J., & Bongers, R. M. (2018). Development of reaching during mid-childhood from a Developmental Systems perspective. PLoS ONE, 13(2), e0193463.
Golenia, L., Schoemaker, M. M., Otten, E., Tuitert, I., & Bongers, R. M. (2018). The development of consistency and flexibility in manual pointing during middle childhood. Developmental Psychobiology, 60(5), 511‑519.
Greve, C., Zijlstra, W., Hortobagyi, T., & Bongers, R. M. (2013). Not all is lost: old adults retain flexibility in motor behaviour during sit-to-stand. PLoS One, 8(10), e77760.
Greve, C., Hortobàgyi, T., & Bongers, R. M. (2015). Physical demand but not dexterity is associated with motor flexibility during rapid reaching in healthy young adults. PLoS One, 10(5), e0127017.
Greve, C., Hortobágyi, T., & Bongers, R. M. (2019). Flexibility in joint coordination remains unaffected by force and balance demands in young and old adults during simple sit-to-stand tasks. European Journal of Applied Physiology, 119(2), 419-428.
Haken, H. (1977). Synergetics, an Introduction: Non-Equilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology. Springer: Berlin/Heidelberg, Germany.
Haken, H., Kelso, J. A. S., & Bunz, H. (1985). A theoretical model of phase transitions in human hand movements. Biological Cybernetics, 51(5), 347‑356.
Hasanbarani, F., & Latash, M. L. (2020). Performance-Stabilizing Synergies in a Complex Motor Skill : Analysis Based on the Uncontrolled Manifold Hypothesis. Motor Control, 24(2), 238‑252.
Iino, Y., Yoshioka, S., & Fukashiro, S. (2017). Uncontrolled manifold analysis of joint angle variability during table tennis forehand. Human Movement Science, 56, 98‑108.
Kang, N., Shinohara, M., Zatsiorsky, VladimirM., & Latash, MarkL. (2004). Learning multi-finger synergies : An uncontrolled manifold analysis. Experimental Brain Research, 157(3).
Kelso, J. A. S., Tuller, B., & Fowler, C. A. (1982). The functional specificity of articulatory control and coordination. Journal of the Acoustical Society of America. 72, S103.
Krishnamoorthy, V., Latash, M. L., Scholz, J. P., & Zatsiorsky, V. M. (2003). Muscle synergies during shifts of the center of pressure by standing persons. Experimental Brain Research, 152(3), 281‑292.
Krishnamoorthy, V., Yang, J.-F., & Scholz, J. P. (2005). Joint coordination during quiet stance : Effects of vision. Experimental Brain Research, 164(1), 1‑17.
Krishnamoorthy, V., Zatsiorsky, V. M., Latash, M. L., & Scholz, J. P. (2004). Muscle modes during shifts of the center of pressure by standing persons : Effect of instability and additional support. Experimental Brain Research, 157(1), 18‑31.
Krüger, M., Eggert, T., & Straube, A. (2013). Age-Related Differences in the Stabilization of Important Task Variables in Reaching Movements. Motor Control, 17(3), 313‑320.
Latash, M. L., Scholz, J. F., Danion, F., & Schöner, G. (2002). Finger coordination during discrete and oscillatory force production tasks. Experimental Brain Research, 146(4), 419‑432.
Latash, M., Scholz, J., Danion, F., & Schöner, G. (2001). Structure of motor variability in marginally redundant multifinger force production tasks. Experimental Brain Research, 141(2), 153‑165.
Latash, M.L., Scholz, J.P., & Schöner, G. (2007). Toward a new theory of motor synergies. Motor Control. 11: 276-308.
Montull, L., Passos, P., Lluís Rocas, Milho, J., & Natàlia Balagué. (2020). Proprioceptive Dialogue -Interpersonal Synergies During a Cooperative Slackline Task.
Madarshahian, S., & Latash, M. L. (2021). Synergies at the level of motor units in single-finger and multi-finger tasks. Experimental Brain Research, 239(9), 2905‑2923.
Maldonado, G., Bailly, F., Souères, P., & Watier, B. (2018). On the coordination of highly dynamic human movements : An extension of the Uncontrolled Manifold approach applied to precision jump in parkour. Scientific Reports, 8, 12219.
Möhler, F., Fadillioglu, C., Scheffler, L., Müller, H., & Stein, T. (2022). Running-Induced Fatigue Changes the Structure of Motor Variability in Novice Runners. Biology, 11(6), 942.
Möhler, F., Marahrens, S., Ringhof, S., Mikut, R., & Stein, T. (2020). Variability of running coordination in experts and novices : A 3D uncontrolled manifold analysis. European Journal of Sport Science, 20(9), 1187‑1196.
Möhler, F., Ringhof, S., Debertin, D., & Stein, T. (2019). Influence of fatigue on running coordination : A UCM analysis with a geometric 2D model and a subject-specific anthropometric 3D model. Human Movement Science, 66, 133‑141.
Möhler, F., Stetter, B., Müller, H., & Stein, T. (2021). Stride-to-Stride Variability of the Center of Mass in Male Trained Runners After an Exhaustive Run : A Three Dimensional Movement Variability Analysis With a Subject-Specific Anthropometric Model. Frontiers in Sports and Active Living, 3, 665500.
Monaco, V., Tropea, P., Rinaldi, L. A., & Micera, S. (2018). Uncontrolled manifold hypothesis : Organization of leg joint variance in humans while walking in a wide range of speeds. Human Movement Science, 57, 227‑235.
Morrison, A., McGrath, D., & Wallace, E. S. (2016). Motor abundance and control structure in the golf swing. Human Movement Science, 46, 129‑147
Murray, R., Zexiang L, Sastry, S.S. (1994). A mathematical introduction to robotic manipulation. CRC Press, London
Nakano, N., Iino, Y., Inaba, Y., Fukashiro, S., & Yoshioka, S. (2022). Utilizing hierarchical redundancy for accurate throwing movement. Human Movement Science, 81, 102918.
Nisky, I., Hsieh, M. H., & Okamura, A. M. (2014). Uncontrolled Manifold Analysis of Arm Joint Angle Variability During Robotic Teleoperation and Freehand Movement of Surgeons and Novices. IEEE transactions on bio-medical engineering, 61(12).
P. Morasso (1981). Spatial control of arm movements. Experimental Brain Research. 42(2): 223-227.
Park, J., Jo, H. J., Lewis, M. M., Huang, X., & Latash, M. L. (2013). Effects of Parkinson’s disease on optimization and structure of variance in multi-finger tasks. Experimental brain research. Experimentelle Hirnforschung. Experimentation cerebrale, 231(1), 51‑63.
Park, J., Lewis, M. M., Huang, X., & Latash, M. L. (2013). Effects of olivo-ponto-cerebellar atrophy (OPCA) on finger interaction and coordination. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology, 124(5), 991‑998.
Park, J., Lewis, M. M., Huang, X., & Latash, M. L. (2014). Dopaminergic modulation of motor coordinaton in Parkinson’s disease. Parkinsonism & related disorders, 20(1), 64‑68.
Passos, P., Milho, J., & Button, C. (2018). Quantifying synergies in two-versus-one situations in team sports : An example from Rugby Union. Behavior Research Methods, 50(2): 620‑629.
Qu, X. (2012). Uncontrolled manifold analysis of gait variability : Effects of load carriage and fatigue. Gait & Posture, 36(2), 325‑329.
Reimann, H., & Schöner, G. (2017). A multi-joint model of quiet, upright stance accounts for the “uncontrolled manifold” structure of joint variance. Biological Cybernetics, 111(5), 389‑403.
Rein, R., Bril, B., & Nonaka, T. (2013). Coordination strategies used in stone knapping : Coordination Strategies Used in Stone Knapping. American Journal of Physical Anthropology, 150(4), 539‑550.
Reisman, D. S., & Scholz, J. P. (2006). Workspace location influences joint coordination during reaching in post-stroke hemiparesis. Experimental brain research. Experimentelle Hirnforschung. Experimentation cerebrale, 170(2), 265‑276.
Riley, M.A., Richardson, M.J., Shockley, K., Ramenzoni, V.C. (2011). Interpersonal synergies. Frontiers in Psychology. 2(38).
Robalo, R., Diniz, A., Milho, J., Pitacas, P., & Passos, P. (2021). Are synergies continuously present in cyclical movements? An example with the basketball dribble task. Human Movement Science, 80, 102883.
Robert, T., Bennett, B. C., Russell, S. D., Zirker, C. A., & Abel, M. F. (2009). Angular momentum synergies during walking. Experimental Brain Research, 197(2), 185‑197.
Saltzman, E., Kelso, J.A.S. (1987). Skilled actions. A task-dynamic approach. Psychological Review. 94: 84-106.
Sanders, R. H., Button, C., & McCabe, C. B. (2020). Variability of upper body kinematics in a highly constrained task – sprint swimming. European Journal of Sport Science, 20(5), 624‑632.
Scholz, J. P., Kang, N., Patterson, D., & Latash, M. L. (2003). Uncontrolled manifold analysis of single trials during multi-finger force production by persons with and without Down syndrome. Experimental Brain Research, 153(1), 45‑58.
Scholz, J. P., Schöner, G., & Latash, M. L. (2000). Identifying the control structure of multijoint coordination during pistol shooting. Experimental Brain Research, 135(3), 382‑404.
Scholz, J., Reisman, D., & Schöner, G. (2001). Effects of varying task constraints on solutions to joint coordination in a sit-to-stand task. Experimental Brain Research, 141(4), 485‑500.
Scholz, J.P., Schöner, G. (1999).The uncontrolled manifold concept: identifying control variables for a functional task. Experimental Brain Research. 126: 289-306.
Schöner, G. (1990). A dynamic theory of coordination of discrete movement. Biological Cybernetics. 63(4): 257-270.
Schöner, G. (1995). Recent development and problems in human movement science and their conceptual implications. Ecological Psychology. 7(4): 291-314.
Serrien, B., Witterzeel, E., & Baeyens, J.-P. (2018). The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy. Journal of Functional Morphology and Kinesiology, 3(3), 48.
Shafizadegan, Z., Sarrafzadeh, J., Farahmand, F., Salehi, R., & Rasouli, O. (2022). Uncontrolled manifold analysis of gait kinematic synergy during normal and narrow path walking in individuals with knee osteoarthritis compared to asymptomatic individuals. Journal of Biomechanics, 141, 111203.
Shafizadegan, Z., Sarrafzadeh, J., Salehi, R., Farahmand, F., & Rasouli, O. (2022). The Effects of Challenging Walking Conditions on Kinematic Synergy and Stability of Gait in People with Knee Osteoarthritis : A Study Protocol. Advanced Biomedical Research, 11, 35.
Shaklai, S., Mimouni-Bloch, A., Levin, M., & Friedman, J. (2017). Development of finger force coordination in children. Experimental Brain Research, 235(12), 3709‑3720.
Shinohara, M., Scholz, J. P., Zatsiorsky, V. M., & Latash, M. L. (2004). Finger interaction during accurate multi-finger force production tasks in young and elderly persons. Experimental Brain Research, 156(3), 282‑292.
Turvey, M.T. (1990). Coordination. American Psychologist. 45(8): 938-953.
Valk, T.A., Mouton, L.J. E. Otten, E., Bonger, R.M (2019) Synergies reciprocally relate end-effector and joint-angles in rhythmic pointing movements. Scientific Reports. 9:17378
Van der Steen, M. M. C., & Bongers, R. M. (2011). Joint angle variability and co-variation in a reaching with a rod task. Experimental Brain Research, 208(3), 411-422.
Wissing, M. B. G., Golenia, L., Smith, J., & Bongers, R. M. (2020). Adjustments in end-effector trajectory and underlying joint angle synergies after a target switch : Order of adjustment is flexible. PLoS ONE, 15(9), e0238561.
Wu, J., McKay, S., & Angulo-Barroso, R. (2009). Center of mass control and multi-segment coordination in children during quiet stance. Experimental Brain Research, 196(3), 329‑339.
Appendix
The appendix presents the different domains of study in which the UCM is employed in the past 20 years.