Dynamic touch-theory
Authors: Dr. David Travieso (UAM)
The following REPAIRS toolbox is available under the CC-BY licence (Creative- Commons: https://creativecommons.org/). This implies that others are free to share and adapt our works under the condition that appropriate credit to the original contribution (provide the name of the REPAIRS consortium and the name the authors of the toolbox when available, and a link to the original material) is given and indicate if changes were made to the original work.
This toolbox describes a practical session for instructing characteristics of dynamic touch. It contains a part where the conceptual background of dynamic touch is presented from a systems perspective. Moreover, it contains the instructions for a practical session that can be used when teaching about the dynamic touch together with links where the required materials can be obtained from (LINK).
One can only conclude that the judgment is based on information, not on the sensations. The stimulus information from wielding can only be an invariant of the changing flux of stimulation in the muscles and tendons, an exterospecific invariant in this play of forces. (Gibson, 1966, p. 127)
When an object is grasped and moved about, “the grasper” (hand, arm, body) is touching only a part of the object. Despite this restriction, the grasper, be it hand, arm, or body, is affected by the whole object. The grasper is not touching the object’s length but somehow length matters. Nor is the grasper touching width, shape, weight, or orientation; nonetheless all matter to perception of the object, to perception of its affordances. (Carello & Turvey, 2017, p. 99)
Dynamic touch as a paradigmatic case for Perception and action Learning from a Systems Perspective
Introduction
a. Perception and action, dynamic touch, and the principles of Ecological Psychology.
Studying Perception and Action Learning from a Systems Perspective involves an intimate conception of two processes that have traditionally been studied independently. This stands in sharp contrast to classic theories of human cognition that have considered perception and action as sequential processes, that is, we need to perceive the environment around us to move effectively. Also relevant for the current toolbox is that under the Aristotelian tradition the human being is conceived has having five senses, namely, vision, audition, touch, smell, and taste, that allow us to perceive the environment around us. These senses, in turn, have different sense organs and neurological pathways that give rise to qualitatively different experiences.
Along this toolkit, we will try to show, through hands-on demonstrations, that perception and action are intimate processes whose profound working can only be understood superficially through independent analysis, and that even the five senses doctrine must be questioned. Do we have more than 5 senses, then? If you check on a web browser about a possible sixth sense, and after trashing telesensation and intuition entries, you will probably end up with proprioception as a candidate, grouping our abilities to sense the inner body and our body position. But this is not what perception-action paradigms are proposing.
As a first intuition, grasp a pen from your scriptory, and holding it by its middle with an index finger and thumb grip, start to swing it with eyes closed. You will be able to feel the effort you make to do this, and you will also feel the swinging pen (at least to the extent that there is “pen” swinging at both sides of your grip). If you now move the grip to one of the sides of the pen, and repeat the swinging movement, the effort has changed (is bigger!), and you can feel the pen swinging only at one side of your grip. Or just hold the pen with the same grip at the middle of the pen without moving it. Does it feel the same as when moving?
If we analyze this simple example under the 5 senses view of perception, their receptors, and neural pathways, do we perceive the pencil through touch, as commonly assumed? The fact that the sensory surface (the fingertips) remains the same across the different grips, and that the perception of effort is present in these conditions, prevents a positive answer. How can we perceive the distal part of the pen (i.e., the swinging part) without getting in contact to it? And why does our perception of the pen change when no swing is applied? It is undoubtful that the so-called proprioception has a role in this situation. But proprioception is supposed to inform us on our inner body and positions…
As we have seen, while wielding the pen it is possible to feel its length without getting in contact with those parts while touching. This simple experience is difficult to understand without the concepts of exteroception and exprorioception (Lee, 1978; Pagano, Carello, & Turvey, 1996). That is, while wielding the pen, we can perceive both the pen (even the part of the pen with which we are not in direct contact), and our own fingers and effort. The perceptual system that allows both perceptions is dynamic touch (Gibson, 1966).
Before describing dynamic touch and its functioning, we would like to say some words about the theory that has supplied us with the concepts necessary for understanding it. This theory is the ecological theory of perception, enunciated by J.J. Gibson (1966; 1979). As an abbreviate introduction, this theory stated, first, that perception is direct. That is, our perceptual systems are able to detect the relevant information for the effective control of our movements without intermediate steps that require interpretation of the stimulus as is done with classic theories of perception.
In other words, classic theories of perception adhere to what Gibson called “the poverty of the stimulus doctrine”, by which the sense data are insufficient and ambiguous with respect to the objective properties of the environment. Thus, for example, we capture the 3D space around us through the projection of light in a 2D surface in our retinas. Therefore, we use “cues” to derivate depth perception. The ecological theory proposes that this is the effect of a passive and elementarist conception of perception. The dynamic and joint work of perception and action, and the presence of high-order variables in the ambient energy arrays give us specific information about our environment without the need of further assumptions like representations and inference (Mantel et al, 2015). This information is called invariants in the ecological tradition, and following Richardson et al. (2008) they can be defined as:
“lawfully structured information (…) that invariantly specifies features (capabilities) of a particular perceiving-acting agent in relation to features of a particular substance, surface, object, or event” (p.179).
For ecological psychology, a second theoretical doctrine that supports the indirect character of classic theories of perception is about the features of objects that are perceived. From the psychophysical tradition in Psychology (one of the classic theories of perception), the study of perception has been the study of our sensitivity to the properties of objects as described by physics, that is, their length, mass, hardness, etc. On the contrary, for ecological psychology perception it is the detection of specific information that allows the control of actions. It is said, therefore, that what we perceive are affordances, defined as the possibilities for action that a certain object allows the perceiver.
Let us instantiate this theoretical disquisition through hands-on demonstrations using dynamic touch as a paradigmatic case.
b. What is dynamic touch?
In a seminal article on dynamic touch, Solomon & Turvey (1988) showed that we can perceive the length of an unseen rod that was wielded from a grasp at one of its ends. More concretely they entitled the paper as “Haptically perceiving the distances reachable with hand-held objects”, a title that reflects how deeply rooted their approach was in the ecological tradition. How could it be that we perceive the length of and object without seeing it or touching its ends?
Their answer is that the perceptual system responsible for the ability perceive the length of an object without seeing it or touching its ends is dynamic touch (Turvey, 1996; Turvey & Carello, 2011; Carello & Turvey, 2017). It is a subsystem, or form, of touch that traverses the traditional separation of senses in touch and proprioception. In fact, dynamic touch is equivalent to effortful touch, or the perception of properties of external objects (exteroception) through the detection of the muscular effort exerted to move them.
Along the last 35 years, plenty of reported research has shown that, through dynamic touch, we are able to perceive not only length (Solomon & Turvey, 1988; Carello et al., 1998), but other object properties like mass distribution (Harrison et al. 2011; van de Langenberg, Kingma, & Beek, 2006), form (Burton, Turvey, & Solomon, 1990; Turvey et al., 1992), or our body position both with respect to the handled object (the grasp) and limb orientation in space (Pagano, & Turvey, 1995; Pagano, Carello & Turvey, 1996). It also shows that we can perceive those properties performing plenty of different amount of torques and producing different movements. Moreover, dynamic touch perception is not restricted to the hand and can be done with other body parts (Hajnal et al., 2007; Wagman & Hajnal, 2014).
Does it mean that the length of a hand-held object affects the effort exerted to wield it? or, more precisely, which is the information that specifies those properties when wielding objects?
c. Perceptual Information and exploratory actions
When wielding a hand-held object we produce different torques, depending on grip position that affects rotational motions. Which might be the invariant information that relates torques and motions in that situation? According to the laws of rigid body motion, the different grip positions, the torques exerted, and the resulting rotational movements, are lawfully related by the moments of the mass distribution of the object.
Thus, the 0th moment of mass distribution quantifies an object’s resistance to being translated; that is, its mass.
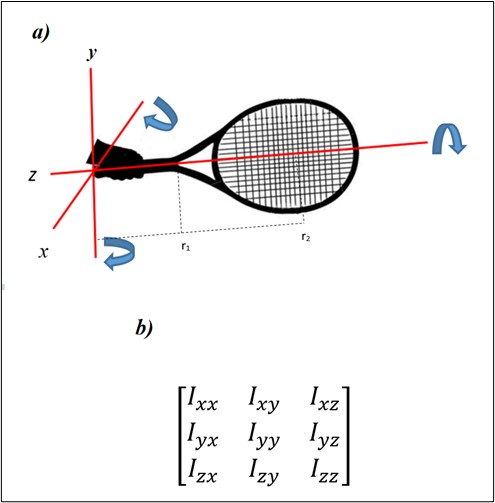
The 1st moment of mass distribution quantifies the torque needed to maintain an object against gravity; that is, the static moment. Finally, the 2nd moment of mass distribution quantifies an object’s resistance to rotational acceleration about an axis; that is, the moment of inertia (see equations 1 to 3, and figure 1 From Carello & Turvey, 2017).
0th = Σmn [1]
1st = Σ(mn ∙ rn) [2]
2nd = Σ(mn ∙ rn2) [3]
All these quantities are invariants that result from the mass distribution of the object along its volume.
(See Figure 1 from Carello & Turvey, 2017)
https://www.tandfonline.com/doi/pdf/10.1080/10407413.2017.1297188
To further understand the notion of moment of inertia we introduce the notion of the so-called Inertia Tensor, which is a 3×3 matrix including the moments of inertia for a certain 3D rotational axes system in which the object is located.
So, similarly to the role of mass (m) in the equation that relates forces and acceleration:
F = m ∙ α [4]
The Inertia tensor (I) relates torques (τ) and rotational acceleration (α):
τ = Ι ∙ α [5]
The orientations of those axes are called the eigenvectors of the inertia tensor, whereas their values in the matrix are called their eigenvalues. These orthogonal axes are represented in the diagonal values, and they are called the principal moments of Inertia, whereas the elements out from the diagonal are the products of inertia and describe resistances in directions different to the principal axes. Finally, the orientation of the axes system can be rotated to its symmetry axes, leaving only the principal moments of inertia. This result in a diagonalization of the matrix, in which the products of inertia are zeroed out (see figure 1 from Carello & Turvey, 2017).
The most extended form of the research line that has studied if we estimate the object properties through the moments of mass distribution uses a psychophysical technique called production of magnitudes. In a prototypic task, participants are asked to reproduce the perceived length of a hand-held object (i.e., a rod) that is out of sight, putting a surface at the perceived distance it reaches.
(see figure 2 from Turvey, 1996 – https://doi.org/10.1037/0003-066X.51.11.1134).
Results showed that perceived length linearly matches objective length of the rod. More interestingly, when different weights (through rings) are added to the rods, participants perceived the rods as longer. Most important, despite differences in perceived length when weights are added, or the rod is grasped from different positions, all estimations can be predicted when using the I1, the first moment of inertia.
(see figure 4 from Turvey, 1996 – https://doi.org/10.1037/0003-066X.51.11.1134).
Thereby, it has been shown, for example, that the estimation of length is mainly linked to I1 (Ixx), whereas the perception of width is linked to I3 (IZZ). However, it has also been shown that it is possible to accurately estimate length statically, accessing static moment as invariant information (Kingma, Van De Langenberg, & Beek, 2004).
Another interesting point is that, as we have already seen, it is possible to diagonalize the inertia tensor. When doing so, only the principal moments of inertia are maintained, zeroing out the products of inertia. Most important, this abstract rotation of the spatial axes can be performed through the wielding movements of the perceiver. Thus, Arzamarski et al. (2010) showed that when a perceiver is asked to report the length of an object, a quantity linked to I1, they produce torques over the antero-posterior axes, implicating the length in the object resistance to rotation (see figures 8 and A1 from Arzamarski et al., 2010). On the contrary, when perceivers were asked to report the width of the objects, they mainly produce torques on the twist axis of the object, accessing then to I3. Moreover, van de Landenberg, Kingma, and Beek (2006) have shown that the use of different mechanical invariants is linked to the exploratory style and the object’s properties, so that there is an interplay of the object’s mass distribution, the way it is explored, and the salience of the mechanical invariants.
(see figures 8 and A1 from Arzamarski et al., 2010) https://link.springer.com/content/pdf/10.3758/APP.72.3.721
Returning to our fundamental questions, it is important to recall that given that torques and resulting rotational acceleration are needed to instantiate the information that specifies the object properties, we are confronted to a perceptual situation in which perception and action cannot be dissociated as independent processes.
An incoming question is, then, whether we are tuned to these mechanical invariants or we learn to perceive such invariants. In other words, if there is perceptual learning in dynamic touch.
d. Perceptual learning in dynamic touch
Given that exploratory actions are needed to instantiate perceptual information, we can assert that perception through dynamic touch cannot be a single function of the sensitivity of touch, as skin spatial and pressure acuity, but also of proprioception and exploratory skills. Moreover, learning cannot be described as a function of the inferential or computational abilities of the perceiver, from skin sensations to mechanical invariants, but they should be merely conceived as the ability to exert torques and produce movements that instantiate the invariants properties and allow their detection.
In fact, perceptual learning has been described in dynamic touch tasks. Let us review some examples. Withagen and Michaels (2005) gave feedback to participants in a length perception through dynamic touch study. They showed that length perception improved throughout the task with veridical feedback. They differentiate two learning processes, attunement and calibration. Attunement describes the process of changing the informational variable used to solve the task, whereas calibration refers to the scaling of perceptual judgements to the informational variable. As we have seen, several candidates (mass, static moment and moment of inertia) give invariant information on the object properties. Thus, Withagen and Michaels gave different feedback to the participants. On one condition they gave feedback on the accuracy of the estimations, giving rise to improvements through recalibration. On the other condition, they informed if two rods were wrongly perceived as having the same length, giving rise to changes in variable use, or re-attunement. Subsequently, Michaels et al. (2008) applied the direct learning theory to dynamic touch. This learning theory established that the mechanical invariants that act as information variables can be described in an informational space where the perceivers use feedback to improve through changes oriented to the most useful informational variables. Finally, and most important, Arzamarski et al. (2010) replicated the use of feedback to promote the change to the most useful informational variables, and they showed that those changes were accompanied by changes on the type of torques exerted on the objects, as we saw in the previous point.
In the next chapter, we will try to introduce some demonstration that will allow to experience the main phenomena and concepts in dynamic touch. These demonstrations can be used in a class to explain concepts and phenomena of dynamic touch.